Dirac Delta Function

Origin

Named for Paul Dirac.

Definition

The Dirac Function as used in engineering is not rigorously mathematically defined. It is supposed to have the following two constraints simultaneously,

$$\delta (x)=\{\begin{array}{l}\infty ,x=0\\ 0,x\ne 0\end{array}{\int }_{-\infty }^{\infty }\delta (x)dx=1$$

Mathematicians have pointed out¹ that it is impossible for a function to satisfy both of these conditions simultaneously, because the integral would evaluate to zero. Dirac himself responded to this critique by instead formulating his function as a “generalized function” or distribution (i.e. not itself a function but a class which encompasses many functions), and proposing that his integral should be interpreted as,

$${\int }_{-\infty }^{\infty }\delta (x)dx=\underset{ϵ\to 0^{+}}{\lim }{\int }_{-\infty }^{\infty }{\delta }_{ϵ}(x)dx$$

where ${\delta }_{ϵ}(x)$ is any function which satisfies

$$\underset{ϵ\to 0^{+}}{\lim }{\delta }_{ϵ}(x)=\{\begin{array}{l}\infty ,x=0\\ 0,x\ne 0\end{array}$$ $${\int }_{-\infty }^{\infty }{\delta }_{ϵ}(x)dx=1$$

So the delta function could be any function which always has an area of one, and which approaches infinity as some quantity associated with it, $ϵ$, approaches zero. It could be the Gaussian normal function, ${\delta }_{ϵ}(x)=\frac{1}{ϵ\sqrt{\pi }}{e}^{\frac{-x^2}{{ϵ}^2}}$, a box function, ${\delta }_{ϵ}(x)=\{\begin{array}{l}\frac{1}{2ϵ},|x|<ϵ\\ 0,otherwise\end{array}$ , or a triangular function, ${\delta }_{ϵ}(x)=\{\begin{array}{l}\frac{1}{ϵ}\left(1-\frac{|x|}{ϵ}\right),|x|<ϵ\\ 0,otherwise\end{array}$. In undergrad I was taught the delta function visually, shown how some functions can be made taller and thinner at the same time, and that at the limit, the function can be infinitely tall and infinitesimally thin, thereby representing an ‘impulse’ signal.

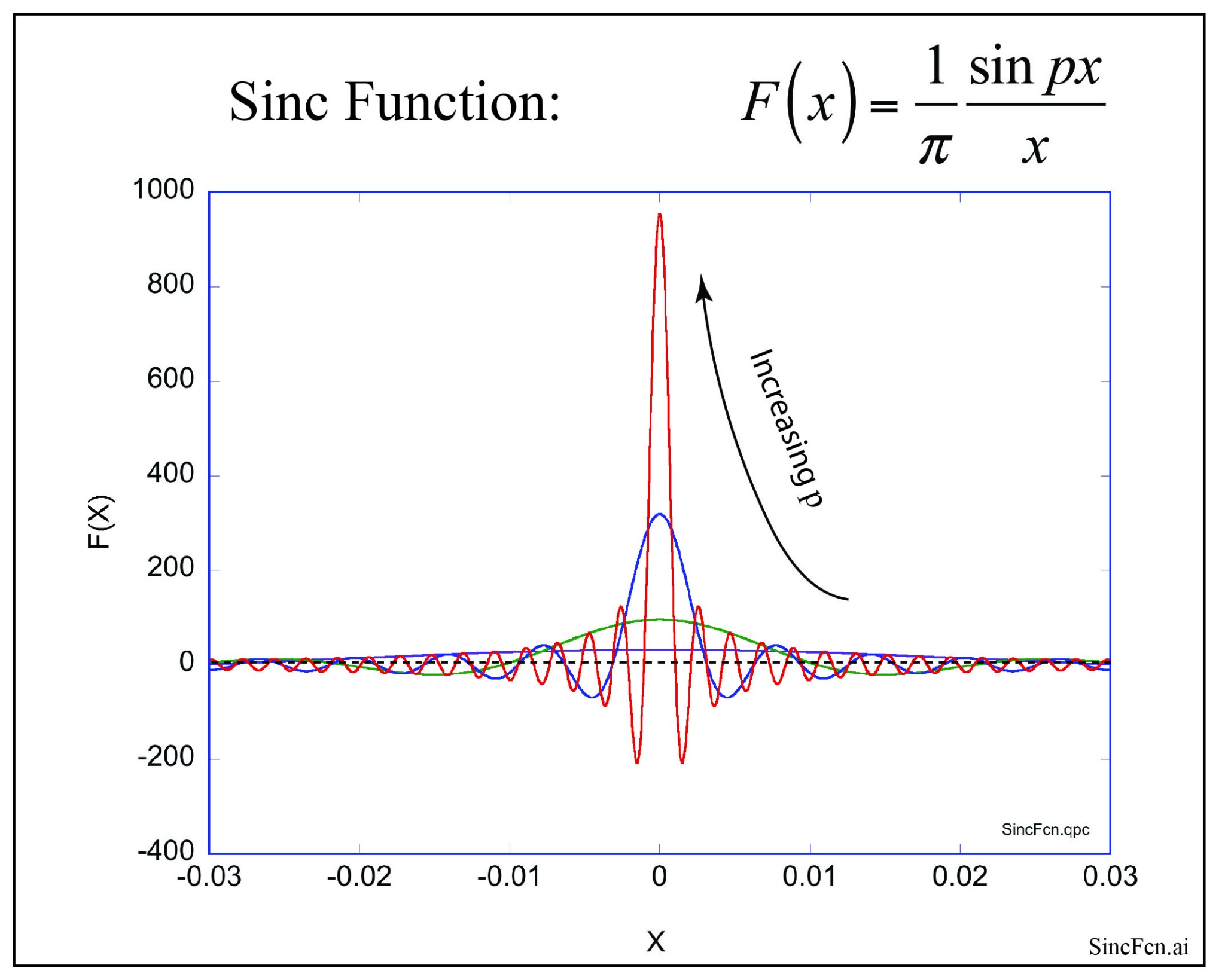
In engineering, we accept this function without mathematical rigor as a useful tool that gets the job done. We also commonly define it slightly differently to the above:

$$\delta (x)=\{\begin{array}{l}1,x=0\\ 0,x\ne 0\end{array}{\int }_{-\infty }^{\infty }\delta (x)dx=1$$

that is to say, we take it to be equal to one at a single point, and not infinity. This change is useful in helping integrals to converge.

Properties

Symmetry:

$$\delta (x)=\delta (-x)$$

Scaling:

$$\delta (ax)=\frac{\delta (x)}{|a|},a\ne 0$$

Differentiation:

$${\delta }^{\prime }(x)=-{\delta }^{\prime }(-x)or{\delta }^{\prime }(-x)=-{\delta }^{\prime }(x)$$

Translation:

$${\int }_{-\infty }^{\infty }f(x)\delta (x-a)dx=f(a)$$

In a graphing context, the delta function can be translated by subtracting some number from its argument: $\delta (x)\to impulseat0$, $\delta (x-2)\to impulseat+2$, $\delta (x-c)\to impulseatc$. Multiplying this impulse with another function in an integral will evaluate that other function at the location of the impulse, as shown above in the Translation property.

The Heaviside Step Function

The Heaviside Step Function is the integral of the Dirac Delta Function, and the delta function is the derivative of the step function:

$$H(x-c)={\int }_{-\infty }^x\delta (s-c)ds\frac{d}{dx}H(x)=\delta (x)$$

Note the value of $x$ as the upper bound of the integral: if we stop integrating before reaching the delta function, i.e. $x<c$, then the integral evaluates to zero, otherwise it evaluates to one.

Uses

See Convolution.

Further Reading

1. Dirac Delta Function by Alan Chang
2. Paul Dirac’s Delta Function by David Nolte
3. Lecture Notes on the Dirac Delta Function, Fourier Transform, Laplace Transform by Luca Salasnich
4. Delta Function by Corinne Manogue and Tevian Dray

Footnotes

1. See Lecture Notes on the Dirac Delta Function, Fourier Transform, Laplace Transform by Luca Salasnich, pg. 1 ↩